Review: Debian 5: Lenny
By EricMesa
- 10 minutes read - 2083 wordsDebian…the father and grandfather of many a Linux distro. I think indirectly Debian is probably running on more computers than any other Linux distro. It’s the basis of Ubuntu, Mepis, Xandros, and many others. And many people use Debian where they need a nice, stable distro. The fact that Debian’s stable releases come out every one to two years and remain supported for a year after a new stable version means that it’s the darling distro where stability is needed. As great as Ubuntu is, you just can’t keep updating every 6 months on a production machine. Now, the flipside is that Debian tends to have older software all-around. So it tends to be used more as a server distro than a desktop distro. But more people than you would expect do run it on their desktops. Afterall, what does the latest version of Gnome have that you REALLY, REALLY need?
When I setup my file and print server I chose Debian because it had a minimal installation that you could build from and just add what you needed. Also, at the time, yum upgrades in Fedora were REALLY not supported. (They’re kinda supported now) So I didn’t want to have to connect a monitor to the computer every time I wanted to upgrade. Debian, on the other hand, has a really good rolling release system. For the most part you can just use apt to upgrade and most everything works as it should.
The last time I installed Debian was version 3.x and it was a little intimidating for me. I had only installed Fedora before that and Debian did not have a GUI installer. But I was able to figure it out and get it up and running without too much trouble. Now with Debian 5, there is a GUI installer supported and I want to check it out and see how it compares to Anaconda and the other GUI installers I’ve seen.
[caption id=“attachment_2115” align=“alignright” width=“300” caption=“Debian 5 installation - language selection”]  [/caption]
[/caption]
Debian boots up and I select graphical install. The first thing it asks me to do is select my language. Next comes the localization. It says, since you picked English you probably live in one of these countries. I think that’s pretty neat. And then, since I picked USA, it says I probably want to use the American english keyboard. Quite a nice bit of programming there. I like it! It then started scanning the DVD.
One important thing to mention here before I forget. This version of Debian is a special remix created by the Debian Project Leader specially for Linux Format Magazine. I think the only difference is that it has some extra packages over the normal CD, but that’s it.
Next I can select a hostname for the computer. I leave it at debian, but if it were a real computer I’d give it a name to match my network scheme of Mario characters. The same goes for the domain name. Then I select my timezone. The installer moves onto the disk partitioning step.
I have four choices. Guided - use entire disk, Guided - use entire disk and LVM, Guided - use entire disk and encrypted LVM, and Manual. I would have really like a little bit of text at the bottom explaining what each of these are. Other than that, good on them for all the options. Also, I just noticed that the installation has a “screenshot” button. This is good for those reviewing distros on bare metal instead of in a VM. I choose the first option. Again, they give some really great options here!
[caption id=“attachment_2116” align=“alignleft” width=“300” caption=“Debian 5 - partitioning questions”] 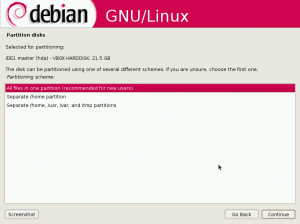 [/caption]
[/caption]
As you can see, there are choices for having everything on one partition, a separate home partition, and separate partitions as you might do in a server setup. Again, this is better than I’ve seen in many of the distros I’ve tested recently. The most amazing thing is that Debian has a reputation for being a lot harder to install than Ubuntu and other distros, but I find these choices very helpful. Again, I would have liked to have had a small explanation for the reasoning behind these diferent choices. Since this is just a review distro, I put everything into one partition. After a confirmation, the disk is partitioned and formatted.
The base system installation also begins at this point. It takes about 10 minutes. Then I put in the root password. Then it asked for my real name, username, and user password. Then it asked if I wanted to add a network mirror as opposed to just installing from the DVD. I hit yes, USA, and then the first Debian repo. It then asked if I wanted to participate in popularity contest. Sure, why not?
Then it gave me a choice of which packages to install. I chose Desktop and Standard System. This took an hour. (remember this is a virtual machine so it may go faster on your computer) Then I installed grub. After rebooting, I had a GDM screen with a very pleasant shade of Blue.
[caption id=“attachment_2124” align=“aligncenter” width=“300” caption=“Debian 5 - GDM”]  [/caption]
[/caption]
I login and I’m greeted with a very nice dekstop theme that matches with the GDM theme.
[caption id=“attachment_2125” align=“aligncenter” width=“300” caption=“Debian 5 - Default Gnome Desktop”]  [/caption]
[/caption]
It appears to be running Gnome 2.22. The latest version which will be going into most of the spring distro releases is 2.26. So they are only 2 versions behind. It’s not TOO bad. Most of the last two releases have been very incremental. With the GIMP they are on version 2.4 - only one version behind. However, version 2.6 was a pretty major upgrade. Inkscape is also available in the graphics category. In the Internet category they have Iceweasel (Firefox) 3.0.6. That’s not too bad. I think with the browser they need to stay up to date because of all the security problems an unpatched browser could cause. They also have Pidgin, Liferea, Evolution, Transmission for BitTorrent, Ekiga for SIP, and Epiphany. Open Office.org is at 2.4. The 3.0 release is supposed to be some hot stuff, so it’s dissapointing that it’s not here. But I think for MOST people, it won’t matter. It should only matter when trading docs with Microsoft users or with very, very complex documents or documents using macros. Rounding things off are Rhythmbox 0.11.6 and Totem 2.22.
So let’s see what version of Blender they have. I go to trusty Synaptic to install the software. It’s at Blender 2.46. This isn’t too old. I think if you aren’t working with the gaming engine, most of the important stuff came in the 2.46 release. Since things are running a bit slow (it’s in a VM), I don’t worry about installing it.
It’s interesting to note that Debian has 22326 packages available for installation! On the one hand, that’s a bit misleading. Debian tends to split up programs into more packages than other distros. For example, for the program blobwars, they have the package blobwars and the package blobwars-data. On the other hand, you have to try REALLY, REALLY hard to find a package not supported by Debian package maintainers. Gwibber isn’t there, but, according to the most recent episode of Linux Outlaws, most distros don’t have it yet. Arch doesn’t. Fedora does. It’s pretty new right now.
Other misc info: Unlike Fedora and (I think) Ubuntu, Debian does not pre-populate your home folder with sub-foldres like Documents, Music, Pictures. Also, it appears that Debian doesn’t have any Mono applications installed by default. By contrast Fedora and Ubuntu have Tomboy installed by default and maybe f-spot. So for those purists who install Ubuntu and then spend hours removing Mono from their systems, perhaps it’d be easier to just run Debian testing.
I decided to check out Debian 5’s version of KDE. I couldn’t figure out the best way to install it so I could get the full KDE experience. So I went to The Debian KDE Maintainers website. They said to use “aptitude install kde-desktop”. So I tried that. That is nearly a gig to download and install. So I let that do its then and went about my buisness. Once I started it up, it brought up the KDE settings wizard. And I was greeted by a familiar scene.
[caption id=“attachment_2133” align=“aligncenter” width=“300” caption=“Debian 5 - KDE Desktop”] 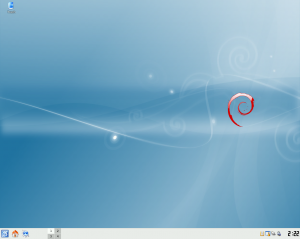 [/caption]
[/caption]
So, Debian has stuck with KDE 3.5. So that’s a potential reason to use Debian - if you really hate KDE 4.x. The KDE install installed tons of programs like Kontact, Kmail, and many other programs starting with the letter K.
So what do I think of Debian? Maybe I’m just getting “old” in the Linux World, but I almost don’t see Ubuntu as being THAT much easier than Debian. Especially with their new (newish) GUI installer, Debian does not deserve to have a reputation as being a lot harder than Ubuntu. Right now, the reason to run Ubuntu rather than Debian is to have the lastest (although not as lastest as Fedora) software. Although I advocated running Debian testing in the previous paragraph, there IS the chance of breakage when running a testing system. So, even though Ubuntu grabs from Debian testing, they then finesse the packages and try to iron out the bugs to make it more stable. To flip-flop once more, there is a distribution called Sidux that runs Debian Unstable, or Sid. So, I guess it’s up to you how bleeding edge you want to be. I would say, if you’re an absolute new user to Linux and it’s important to have the latest packages - check out Linux Mint or Ubuntu. If you’re a new user and want to install your system and then only install security updates - you might want to strongly consider Debian. You’ll have somewhere between 2 and 3 years of security updates before you need to worry about upgrading to the latest version. After all, while 90% of the time an upgrade goes smoothly, you could be in that 10% where it doesn’t - so why upgrade constantly? I know I’m too young to be curmudgeonly, but I’m getting to the point where once I have kids, I might just switch to CentOS or Debian rather than deal with the upgrade crap every six months. When else should you use Debian? If you like the .deb package format better than the .rpm and are running a server - you should use Debian rather than CentOS. If you have a laptop you MIGHT be better served by Ubuntu or Linux Mint. Manufacturers are always changing the underlying chips in their products without changing the outer packaging so a more up to date distro like Ubuntu might have the kernel modules or firmware you need to have wifi enabled. If you have a laptop and never use wifi - then you’re probably fine with Debian.
I don’t want to drag this old argument out again since everything in KDE is supposedly fixed with KDE 4.2 (I haven’t tried it yet). But a lot of people were upset with the move from KDE 3.5. It’ll at least two years before Debian moves to the KDE 4 series, so you can get two more years of KDE if you use Debian. That might apeal to some people.
So, while Debian hasn’t done anything awesome with Lenny that makes it a must-use distro, it has certainly helped raise itself from the too geeky to be of any good status it had before. I think that’s the only thing left for Debian to do. Debian’s marketing team needs to come up with something that makes them special on the desktop (if that is important to them). Right now Fedora owns bleeding edge without being too hard. Arch owns total bleeding edge (seemingly coming out of nowhere). Ubuntu owns newbie distro. openSuse is Microsoft-like and liked by businesses. Right now Debian’s one claim to fame is stability. But, on the whole, I don’t often experience problems with Fedora’s bleeding edge-ness. And I never had any stability problems with Ubuntu. Perhaps one thing Debian could do is steal some of Slackware’s thunder by being the most vanilla. In other words, you get unadulterated Gnome, KDE, and Xfce. For example, Xbuntu mucks about with Xfce’s default look. If Debian already is the most vanilla, they need to do a better job of selling this.